독립변수(1차 함수의 입력값): 공부한 시간이라하고,
종속 변수(1차 함수의 출력값): 성적이라 한다면,
선형 회귀: 공부한 시간에 따른 성적의 변화를 예측한 것이다.
최소 제곱법 (제곱 오차 합)
최소 제곱법은 (실제 성적 - 예측한 성적)²인데, 실제 성적과 예측한 성적이 차이가 안나는게 0이니까 제곱값이 작을수록 예측을 잘 했다는 것이다.
제곱을 사용하는 이유는 (실제성적-예측성적)의 값이 음수가 나오면 둘 사이의 차이가 많이 남에도 불구하고 (-)때문에 결과가 작아질 수 있어 부호를 없애주기 위함이다. 절댓값을 사용해도 되긴 하지만 제곱을 사용한다.
이 최소 제곱법으로 시간에 따른 성적을 예측하려면 x값(입력 값, '공부한 시간')과 y값(출력 값, '성적')을 이용해 직선의 방정식(y=ax+b)을 만든다.
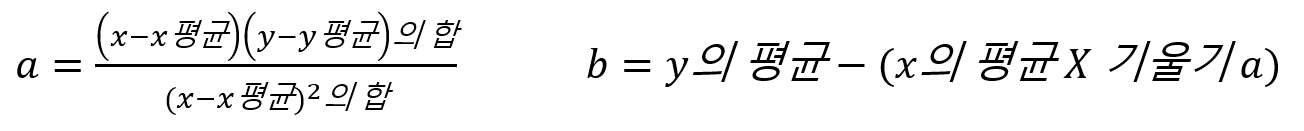
이렇게 만들어진 직선의 방정식을 통해 예측값을 구한다. (이렇게 구한 예측값은 정확하지는 않지만, 제곱법 오차를 최소화 하는 공식으로 만들었기 때문에 제곱법 오차를 최소화한 예측값임)
머신러닝의 원리 자체가 '한번에 정확히 계산하겠다!' 가 아니라 '일단 그리고 조금씩 수정해 나가기' 라서 오차가 최소가 될때까지 계속 수정해가며 최소가 되는 직선의 방정식(기울기, 절편)을 찾는게 우리의 목표이다!
평균 제곱 오차(MSE)
제곱 오차 합을 개수(n)으로 나눠준게 '평균 제곱 오차(MSE)' 이다.
MSE가 작다는건 실제값과 예측값의 차이가 작다는것이고, 최소오차이기 때문에 우리는 mse값이 가장 작게 되는 직선의 방정식(위에서 말한 직선의 방정식)을 찾아가야 한다.
경사 하강법
경사 하강법은 우리가 구해야하는 기울기를 (기울기-오차) 그래프로 나타낸 것으로, 기울기에 해당하는 점에서의 미분값(순간 기울기)이 0이 될 때가 최적의 기울기(m)이다. 우리는 넵 미분값이 0인 a가 최적의 기울기가 되는 값을 찾아야한다.
기울기(a)에 대해서 편미분한 값이
0 → 오차가 최소
양수 → 최적값이 왼쪽에 있다 (지금의 기울기가 너무 크다)
음수 → 최적값이 오른쪽에 있다 (지금의 기울기가 너무 작다)
∴ 우리는 미분값에 따라 a를 증가시킬지 감소시킬지 결정하는게 경사 하강법이다!
원래 미분할땐 x를 기준으로 미분했다면, 편미분은 우리가 핵심적으로 생각하는 값(기울기 or y절편)에 대해 미분하는 것이다.
방정식 ax+b에서 우리가 구하려는건 a와 b지 x가 아니니까 x에 대해서 미분하는게 아니라 기울기를 구할 땐 a, y절편을 구할 땐 b에 대해서 미분하는 것이다.
학습률
학습률은 기울기를 얼마나 변화시킬지를 말한다.
기울기-오차그래프에서 기울기(a)의 이동거리로 직선의 방정식이 최소 오차가 되기 위해서 기울기나 y절편이 더 커져야 하는지 작아져야 하는지를 결정한다.
학습률이 너무 크면 최적의 값에서 더 멀어질 수 있고 (첫번째 그래프),
학습률이 너무 작으면 아래의 그림보다도 더 찔끔찔끔가니까 계산량이 늘어나서 시간이 오래걸리게 된다 (두번째 그래프).
→ 이 학습률에 따라 기울기가 변하기때문에 머신러닝에서 학습률의 값을 적절히 바꾸면서 최적의 학습률을 찾는 것이 중요하다!


y절편(b)에 대한 것도 기울기와 마찬가지로 경사 하강법을 사용해서 구한다. (제대로 된 직선의 방정식 구하려면 기울기와 y절편이 다 중요하기 때문)
평균 제곱 오차가 기울기-오차, y절편-오차 그래프의 이차함수이기 때문에 평균 제곱 오차식에 우리가 예측한값(=직선의 방정식 = ax+b)를 대입해 아래의 식이 나온다.

우리는 학습률을 조정하면서 최적의 기울기와 y절편을 찾아가는 것을 통해 best의 직선의 방정식을 찾아가는 것이다!
회귀 분석 종류
단순 선형 회귀: 공부한 시간(입력값)에 따른 성적(결과) → 입력값 1개에 따른 결과
다중 선형 회귀: 공부한 시간(입력값1), 과외횟수(입력값2)등에 따른 성적(결과) → 입력값2개이상에 따른 결과
이런 단순 선형회귀나 다중 선형회귀는 굳이 머신러닝을 안써도 수학적으로 직선의 방정식을 찾을 수 있지만,
비선형 회귀는 우리가 구해야하는게 몇차 함수인지도 모르기 때문에 사람이 구하긴 너무 어려워 머신러닝을 사용해서 찾아햐 하는 것이다.
